Matematica -I limiti.

I limiti


Se la funzione e' il concetto di base per la matematica il limite e' il concetto di base per le funzioni: infatti e' il limite che ci permette di superare i paradossi dovuti all'insufficienza del concetto di punto perche' ci permette di utilizzare il concetto di intervallo.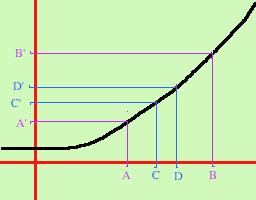


Teoricamente il limite e' una cosa molto semplice: se io considero un piccolo intervallo sull'asse delle x ad esso corrispondera' un intervallo piu' o meno piccolo sull'asse delle y; se quando restringo l'intervallo sull'asse delle x mi si restringe anche l'intervallo corrispondente sull'asse delle y allora ho un limite
In figura all'intervallo in viola AB corrisponde l'intervallo in viola A'B' ed all'intervallo piu' piccolo in blu CD corrisponde un intervallo piu' piccolo in blu C'D'; allora posso avvicinarmi ad un punto quanto voglio: basta rendere sempre piu' piccolo l'intervallo sulle x
Poiche' l'intervallo posso renderlo piccolo quanto voglio allora posso sostituirlo al concetto di punto
Il problema e' tradurre un concetto cosi' semplice in linguaggio matematico.


Limite finito di una funzione in un punto

Il concetto espresso nella pagina precedente e' abbastanza comprensibile, diventa piu' complicato l'esprimerlo in forma matematica
Per prima cosa, siccome si parla di limite di una funzione e la funzione e'come variano i punti sull'asse y partiremo da un intervallo sull'asse y e diremo che allo stringersi di un intervallo sulle y avvicinandosi ad un valore l si stringe anche l'intervallo corrispondente sulle x avvicinandosi ad x0



Per dire questo consideriamo sull'intervallo delle X (quello marcato piu' scuro) un qualunque punto x a cui corrisponde f(x) sull'asse Y. Per rendere piccoli gli intervalli bastera' dire che deve essere piccola la distanza tra f(x) ed l e contemporaneamente la distanza ta x ed x 0; ora la distanza si ottiene facendo la differenza fra le coordinate, ma essendo sempre positiva, dovra' essere presa in modulo. Quindi bastera' dire che quando la distanza sulle Y e' minore di un numero piccolissimo anche la distanza sulle X dovra' essere minore di un numero piccolissimo, od in modo equivalente quando f(x) si avvicina ad l anche x si avvicina ad x0.
Ora siamo pronti a dare la definizione matematica:

Si dice che la funzione y=f(x) ammette limite finito l per x tendente ad x0 e si scrive:
limx->x0 f(x)=l
se per ogni numero positivo (epsilon) piccolo a piacere esiste un numero (delta epsilon cioe' delta dipendente da epsilon) tale che da
|x-x0 | < segua |f(x)-l|<
|x-x0 | < e' un intervallo A sull' asse x, intorno completo del punto x0
|f(x)-l|< e' un intervallo B sull'asse y
quindi si puo' anche dire che quando la x appartiene ad A allora f(x) appartiene ad B
od anche: quando x si avvicina ad x0 allora f(x) si avvicina ad l


Limite di una successione

limite di una successione di numeri reali
Possiamo applicare il concetto di limite ad una successione di numeri reali
Non si fa in tutte le scuole, ma ho visto farlo in alcuni licei scientifici e nei bienni di alcune universita';
Per costruire la matematica possiamo prendere come base i numeri Naturali e poi sviluppare tutta la teoria (metodo classico), oppure possiamo prendere come base il concetto di successione(metodo della scuola russa); il risultato e' del tutto equivalente
Poiche' i numeri reali (e quindi la retta reale) possono essere pensati come limiti di una successione di numeri razionali il concetto di limite diviene una proprieta' intrinseca dei numeri reali stessi


Limite finito di una successione
(limite di una successione convergente)

Facciamo per semplicita' un esempio numerico e consideriamo la successione:
1, 1/2, 1/4, 1/8, 1/16,......
Si vede subito che procedendo nei termini ci avviciniamo sempre di piu' al valore limite zero.
Per impostare la definizione di limite dobbiamo dire che prendendo termini piu' avanzati la differenza fra questi termini e il limite diventera' sempre piu' piccola
Se non sei convinto prova a fare la differenza fra il quinto termine e il limite(zero), poi fra il decimo e il limite, vedrai che la differenza diventa piu' piccola man mano che prendi un termine di ordine superiore
Consideriamo ora la successione generica:
a1 , a2 , a3 , a4 , a5 ,....., an ,....
per indicarla consideriamo il suo termine generico an
diremo che la successione an ammette limite finito l per n --> e scriveremo
lim n --> a n = l
se fissato un numero piccolo a piacere e' possibile trovare un termine della successione tale che per quel termine e tutti i suoi successivi valga la relazione:
| an-l |<

Limite di una successione divergente
Per fare il limite di una successione divergente rifacciamoci al concetto che si ha un limite quando avendo un intervallo che si contrae anche l'intervallo corrispondente si deve contrarre; ora non e' necessario che l'intervallo sia un intorno di un valore finito, ma puo' anche essere un intorno di infinito
Rifacciamoci al caso che la successione tenda a +
Allora potremo dire che la successione a1 , a2 , a3 , a4 , a5 ,....., an ,....
e' divergente (ammette limite infinito) per x-> e scriveremo
lim n --> a n =
se preso n>M esiste in sua corrispondenza un intorno di infinito dipendente da M tale che il termine an ed i suoi successivi siano tutti contenuti in quell'intorno di infinito
o in modo piu' algebrico:
se preso un numero positivo M e' possibile trovare un termine della successione ak tale che per esso e tutti i termini che lo seguono (cioe' che hanno indice maggiore di K) valga la relazione ak>M



Limite destro e limite sinistro

Per capire bene il concetto di limite destro (sinistro) consideriamo cos'e' un intervallo per un punto interno: e' un intorno e per essere un intorno non e' necessario che il punto sia al centro dell'intervallo, anzi il punto puo' essere spostato anche fino al bordo se l'intervallo e' chiuso ed in tal caso avremo un intorno destro o sinistro del punto.
Ora quando considero il limite limx->x0 f(x)=l invece di considerare tutto un intervallo che contenga x0 possiamo considerarne un intorno destro (sinistro) ed in tal caso sull'asse y corrispondera' un intorno destro o sinistro di l ma cio' non cambiera' nulla: infatti allo stringersi dell'intervallo sull'asse delle y corrispondera' lo stringersi dell'intorno sull'asse delle x.
Cioe' quando f(x) si avvicina ad l x si avvicina ad x0
Definizione matematica:
Si dice che la funzione y=f(x) ammette limite finito destro l per x tendente ad x 0+ e si scrive:
limx->x0+ f(x)=l se esiste un numero positivo (epsilon) piccolo a piacere tale che da
|f(x)-l|< segua x-x0 < (delta epsilon cioe' delta dipendente da epsilon)
Note: x tendente ad x0+ significa che mi avvicino ad x da destra, cioe' dalla parte dei valori positivi


l'infinito nei limiti

Il concetto di infinito e' sempre stato un po' la bestia nera della matematica e col concetto di limite si puo' affrontare in modo abbastanza efficace: il limite mi mette in relazione due intervalli che si contraggono contemporaneamente: allora perche' non applicare questo concetto anche ad un intorno di infinito? Il problema e' che non posso far riferimento ad un intorno e nemmeno ad un intervallo, pero' posso fare riferimento al bordo dell'intervallo che, man mano che si stringe, assumera' valori sempre piu' grandi in valore assoluto.
In pratica quando ho un intervallo che si stringe verso infinito devo dire che il suo valore di bordo risulta maggiore di un qualunque numero (di solito indicato con M per le y ed N per le x) grande a piacere se andiamo verso + oppure minore di un numero qualunque numero negativo grande a piacere in valore assoluto se ci spostiamo verso -
Sarebbe bene che provassi ora a ricavare tu i vari casi senza studiarli a memoria, comunque, magari per esercizio, di seguito ti enumero i casi possibili
Distinguiamo tre casi:
limite per x -> c
limite l per x ->
limite per x ->
Se vuoi puoi dare un'occhiata alla tabella riassuntiva dei vari casi
altrimenti fai click qui per passare ai teoremi sui limiti
C'e' ancora da dire che il concetto di limite mi permette di risolvere uno dei problemi piu' spinosi della matematica: la divisione per zero



Teoremi sui limiti
Ora abbiamo un nuovo oggetto base per la matematica, il concetto di limite che sostituira' il concetto di punto, e' quindi necessario riscrivere tutta la matematica da questo punto di vista, ma per partire in modo adeguato dobbiamo fissare bene le proprieta' dei limiti, cioe' individuare dei teoremi che ci serviranno come base per ricostruire l'intera matematica dal nuovo punto di vista
I teoremi sui limiti serviranno a fissare le proprieta' dei limiti stessi, ad essi affiancheremo le operazioni sui limiti che ci permetteranno di riportare le operazioni algebriche anche sul concetto di limite.

Teorema dell'unicita' del limite
Non meravigliatevi del fatto che questi teoremi sembrino una cosa ovvia: e' dovuto al fatto che stiamo riscrivendo le regole di base.
Il teorema dell'unicita' del limite dice che il limite, quando esiste, e' unico, cioe' una funzione non puo' assumere al limite due valori diversi.(in pratica significa che stringendo l'intervallo l'intervallo stesso non si suddivide ma resta tutto unito anche quando diventa piccolissimo; cosa d'altra parte necessaria se vogliamo sostituire il concetto di intervallo al concetto di punto)
Per dimostrarlo basta ragionare per assurdo: supponiamo che non sia vero il risultato e mostriamo che non e' vero il teorema.
se non fosse vero che abbiamo un solo valore ne avremmo due diversi, ma allora questi due valori sarebbero due punti ad una certa distanza, allora se prendiamo epsilon minore di quella distanza l'intervallo non potra' contenere entrambe i limiti e quindi non vale il concetto di limite.
In termini matematici sembra un po' piu' complicato, ma e' la stessa cosa
Supponiamo esistano due limiti e dimostriamo che in tal caso non puo' esistere nessun limite.
I due limiti siano
limx->x0 f(x)=l1
limx->x0 f(x)=l2 con l1<l2
Essendo i due limiti diversi la loro differenza in modulo sara' la distanza
distanza=|l1-l2 |
ora pongo
= | l1-l2 | /2
cioe' scelgo uguale alla meta' della distanza ed il gioco e' fatto: ho creato una coperta troppo corta che non puo' coprire contemporaneamente i due limiti
Ora e' impossibile avere contemporaneamente
|f(x)-l 1 |<
|f(x)-l 2 |<
Perche' l'intervallo non puo' coprire contemporaneamente l 1 ed l 2 in quanto la loro distanza e' maggiore di ed allora non puo' esistere il limite. Come volevamo dimostrare

Teorema della permanenza del segno
Il teorema dice che se una funzione ha limite diverso da zero esiste tutto un intervallo ove la funzione ha lo stesso segno del suo limite.
La dimostrazione e' molto simile a quella del teorema sull'unicita' del limite: bastera' fare una coperta abbastanza stretta che contenga il limite ma non lo zero
Se il limite e' diverso da zero ci sara' una certa distanza fra il limite e lo zero, quindi se consideriamo uguale alla meta' di questa distanza l'intervallo che copre il limite non potra' raggiungere lo zero, pertanto in tutto questo intervallo il segno della funzione sara' uguale a quello del limite

Teorema della maggiorante e della minorante
(Teorema dei "carabinieri")
Il nome esatto sarebbe quello sopra, ma anche in alcuni testi scolastici ho visto chiamare questo teorema col secondo nome, che rende bene l' idea del teorema stesso:
il teorema dice questo
Se abbiamo tre funzioni, la prima maggiore delle altre due (maggiorante) e la terza minore delle altre due (minorante) allora se sia la prima che la terza funzione tendono ad un limite finito l allora anche la seconda deve tendere allo stesso limite
Inutile dire che la prima e la terza funzione fanno da carabinieri e prendono in mezzo la seconda per portarla in prigione nel limite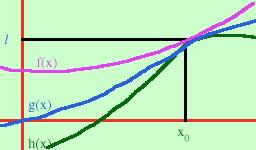



Dirlo in forma matematica e' un po' piu' laborioso
Se abbiamo tre funzioni:
y=f(x) y=g(x) y=h(x)
tali che
f(x)≥g(x)≥h(x)
se abbiamo inoltre che
limx->x0 f(x)=l e limx->x0 h(x)=l
allora vale anche
limx->x0 g(x)=l
Per un accenno di dimostrazione posso dire che prendendo un intorno completo che contenga l per f(x) e prendendo un altro intorno completo che contenga l per h(x) siccome g(x) e' compresa fra le due funzioni bastera' considerare l'intervallo intersezione dei due intorni per avere un intorno completo di l per la funzione g(x)

Operazioni sui limiti
Le operazioni sui limiti ci serviranno per il calcolo degli stessi

Limite di una somma di funzioni
In modo intuitivo possiamo dire che il limite di una somma e' uguale alla somma dei limiti: se ho due funzioni, la prima che tende a 5 e la seconda che tende a 7 per un certo valore di x allora la funzione somma mi tendera' a 12
se ad esempio devo calcolare
limx->0(senx+ex)=
siccome
limx->0senx = 0
limx->0ex= 1
avro'
limx->0(senx+ex)= 0+1=1
In forma matematica dobbiamo invece dire:
Se abbiamo due funzioni y=f(x) y=g(x)
tali che limx->x0 f(x)=l e limx->x0 g(x)=m
allora si ha limx->x0 (f(x)+g(x))=l+m
A scuola (talvolta e non in tutte le scuole) si studia anche la dimostrazione ma ci si limita a questa prima operazione
Intuitivamente prendero' come intervallo per la somma di funzioni la somma dei due intervalli nel modo seguente:
sapendo che (ipotesi)
limx->x0 f(x)=l e limx->x0 g(x)=m
voglio dimostrare che ottengo (tesi) limx->x0 (f(x)+g(x))=l+m
so che limx->x0 f(x)=l equivale a |f(x)-l|< 1
e che limx->x0 g(x)=m equivale a |g(x)-m|< 2
devo dimostrare che con queste ipotesi ottengo
limx->x0 (f(x)+g(x))=l+m che equivale a |f(x)+g(x)-l-m|< 3
DIMOSTRAZIONE

|f(x)+g(x)-l-m| = |(f(x)-l)+(g(x)-m)|
per le proprieta' dei moduli
|(f(x)-l)+(g(x)-m)|<|f(x)-l|+|g(x)-m|<1 +2
Per la proprieta' transitiva della disuguaglianza avremo
|f(x)+g(x)-l-m|< 1 +2
bastera' ora prendere 3 > 1 +2 per ottenere la tesi

Limite di una differenza di funzioni
In modo intuitivo possiamo dire che il limite di una differenza di due funzioni e' uguale alla differenza dei limiti
se ad esempio devo calcolare
limx->1 (ex- logx) =
siccome
limx->1 ex = e
limx->1 log x= 0
avro'
limx->1 (ex - log x)= e-0 = e
In forma matematica dobbiamo dire:
Se abbiamo due funzioni
y=f(x) y=g(x)
tali che
limx->x0 f(x)=l e limx->x0 g(x)=m
allora si ha
limx->x0 (f(x)-g(x)) = l - m


Limite di un prodotto di funzioni
Il limite di un prodotto di funzioni e' uguale al prodotto dei limiti
Se ad esempio devo fare
limx->0 cosx·ex=
siccome
limx->0 cosx = 1
limx->0 ex= 1
avro'
limx->0 cosx·ex= 1·1=1
In forma matematica dobbiamo invece dire:
Se abbiamo due funzioni
y=f(x) y=g(x)
tali che
limx->x0 f(x)=l e limx->x0 g(x)=m
allora si ha
limx->x0 f(x)·g(x)=l·m
Come caso particolare e' da tenere presente il prodotto di una costante per una funzione:
poiche' il limite di una funzione costante resta sempre lo stesso qualunque sia x, avremo che:
se devo calcolare il limite del prodotto di una costante per una funzione bastera' moltiplicare la costante per il limite della funzione ( si usa anche dire che possiamo estrarre le costanti dall'operazione di limite)
esempio
limx->0 5cosx = 5limx->0 cosx = 5

Limite di un quoziente di funzioni
Anche qui possiamo dire che il limite di un quoziente di funzioni e' uguale al quoziente dei limiti, pero' a patto che al limite la funzione al denominatore abbia un valore diverso da zero
Se ad esempio devo fare
limx->0 x/cosx =
siccome
limx->0 x = 0
limx->0 cosx= 1
avro'
limx->0 x/cosx = 0/1=0
se avessi avuto:
limx->0 cosx/x =
non avrei potuto applicare questo teorema perche' al limite il denominatore vale 0
In forma matematica dobbiamo dire:
Se abbiamo due funzioni
y=f(x) y=g(x)
tali che
limx->x0 f(x)=l e limx->x0 g(x)=m e m 0
allora si ha
limx->x0 f(x)/g(x)=l/m
Notare bene quel m 0 nell'ipotesi

Due limiti notevoli
Sono molto importanti: il primo e' alla base del calcolo dei limiti su parecchie funzioni trigonometriche e l'altro e' il generatore del numero e (numero di Nepero)
limx->0 senx/x =
limx->oo (1+1/x)x =

Forme indeterminate
Mediante il concetto di limite e' possibile dare un senso matematico a limiti quali

1/0 =
1/ = 0
/0 =
0/ = 0
· =
Tuttavia vi sono ancora alcune forme cui non possiamo assegnare un valore: le cosiddette forme indeterminate:
Esse vanno trattate caso per caso
Forme indeterminate
0/0
/
0·
-
0 , 1 e 0